游戏掷筛

理论概率论掷筛 NdS

Created At : 2023-08-30 14:28

Count:1.6k Views 👀 :

Comment:

1. 游戏机制中的概率论

1. 游戏机制中的概率论

1.1. 摘要

前言
dota2中暴击率的伪随机性
- 自己手测5组数据
- dota2官方wiki中对伪随机性（PRD）的定义
- 分析c值的计算
游戏中NdS掷骰机制
- 通过掷骰调整事件发生概率更平稳或者更极端
- 通过掷骰调整事件放生概率偏向均值较大或较小的一侧。有三个相关模型
总结

1.2. 前言

在互联网上，充斥着各种抽奖活动：拼多多的一分钱抽奖，微信抽奖，游戏抽奖等等。但是我们能感受到的是：游戏中中奖的概率似乎要高于微信或者拼多多等抽奖的概率。（因为我从未在游戏以外活动中抽到过奖励）。也考虑到游戏如果也和生活中的抽奖那样抽奖都是独立事件，那么运气影响的部分过高，竞技性就会降低，难以留住像我这样的“非酋玩家”。所以游戏中的概率一定不是真随机。

下面就是我通过搜索资料了解到的一些游戏中的概率模型机制。

1.2.1. dota2中暴击率的伪随机性

表1 在裸出一个水晶剑（30暴击率）情况下的20次暴击图表

暴击率的平均值为0.28与30较为接近。

因为自己手测能得到的样本数很少，随机性大。

所以使用dota2wiki随机分布 - Dota 2 Wiki，刀塔百科 (fandom.com)中机制的公式进行代码分析。

这是dota2官方wiki中对伪随机分布(pseudo-random distribution，简称PRD)的定义

表1.1.1 prd下直到下次暴击的攻击次数

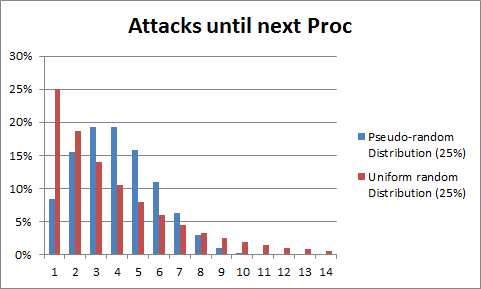
表1.1.2 prd下的触发几率

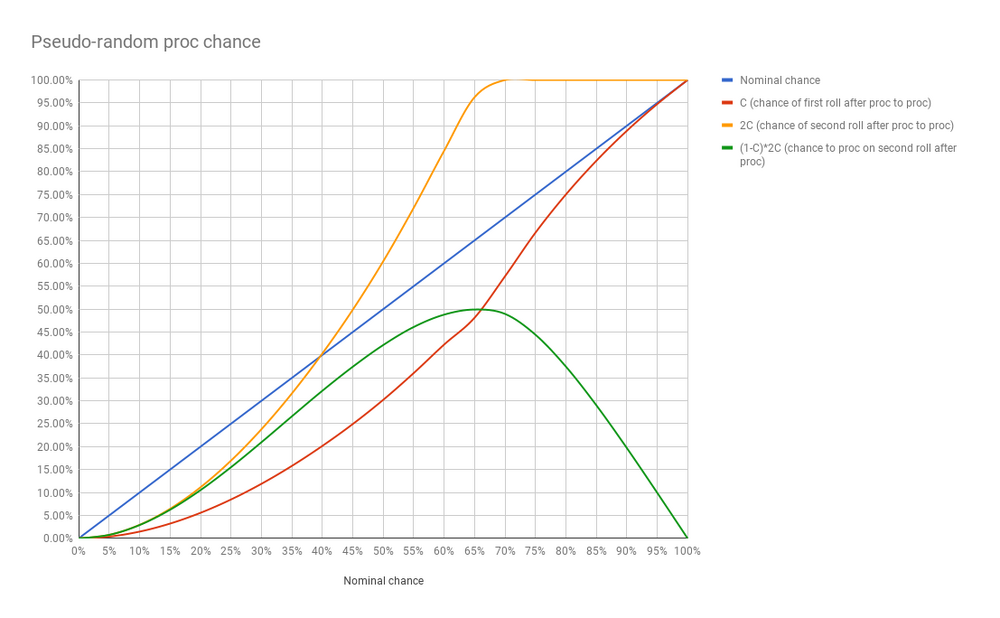
dota2官网中给出的C值

从Calculating the constant C in Dota 2 pseudo-random distribution - Arqade (stackexchange.com)

我们了解到这种伪随机暴击率是以马尔科夫链为理论进行的。

即下一次普通攻击是否暴击仅和这一次是否暴击相关。

例如暴击率为20%，第一次是1*C即5.6%，第二次为11.2%,如此累加，在第五次达到28%，第十次达到56%。当暴击时，暴击率再次从5.6%开始。也就是说更少出现真随机那样连续暴击或者连续不暴击的情况，减少运气成分，使游戏更加公平。

同时，计算C值的c#代码如下

//CfromP是主函数，传入理论概率P就可以求得递增的C值
public decimal CfromP( decimal p )
{
    decimal Cupper = p;
    decimal Clower = 0m;
    decimal Cmid;
    decimal p1;
    decimal p2 = 1m;
    while(true)
    {
        Cmid = ( Cupper + Clower ) / 2m;
        p1 = PfromC( Cmid );
        if ( Math.Abs( p1 - p2 ) <= 0m ) break;

        if ( p1 > p )
        {
            Cupper = Cmid;
        }
        else
        {
            Clower = Cmid;
        }

        p2 = p1;
    }

    return Cmid;
}

private decimal PfromC( decimal C )
{
    decimal pProcOnN = 0m;
    decimal pProcByN = 0m;
    decimal sumNpProcOnN = 0m;

    int maxFails = (int)Math.Ceiling( 1m / C );
    for (int N = 1; N <= maxFails; ++N)
    {
        pProcOnN = Math.Min( 1m, N * C ) * (1m - pProcByN);
        pProcByN += pProcOnN;
        sumNpProcOnN += N * pProcOnN;
    }

    return ( 1m / sumNpProcOnN );
}

结果和dota2官方数据一致：

C(0.05) = 0.003801658303553139101756466
C(0.10) = 0.014745844781072675877050816
C(0.15) = 0.032220914373087674975117359
C(0.20) = 0.055704042949781851858398652
C(0.25) = 0.084744091852316990275274806
C(0.30) = 0.118949192725403987583755553
C(0.35) = 0.157983098125747077557540462
C(0.40) = 0.201547413607754017070679639
C(0.45) = 0.249306998440163189714677100
C(0.50) = 0.302103025348741965169160432
C(0.55) = 0.360397850933168697104686803
C(0.60) = 0.422649730810374235490851220
C(0.65) = 0.481125478337229174401911323
C(0.70) = 0.571428571428571428571428572
C(0.75) = 0.666666666666666666666666667
C(0.80) = 0.750000000000000000000000000
C(0.85) = 0.823529411764705882352941177
C(0.90) = 0.888888888888888888888888889
C(0.95) = 0.947368421052631578947368421`

假设一名英雄有15%的暴击率，连续N次不暴击，之后首次触发暴击所需普攻数dota2中关于暴击/眩晕伪随机概率的玄学及其应用 - 知乎 (zhihu.com)

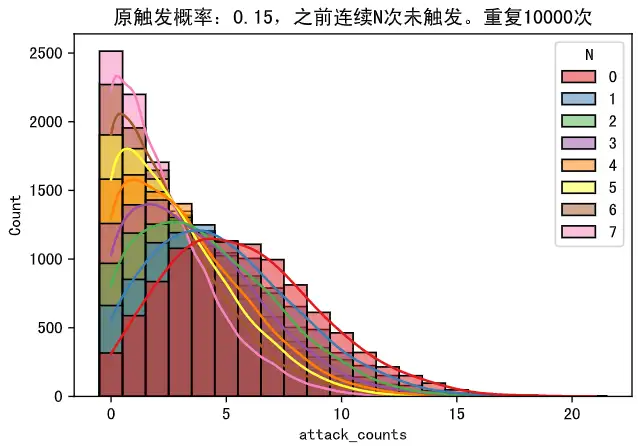
之前连续0次未触发,之后平均需要5.6996次攻击才能触发暴击/眩晕
之前连续1次未触发,之后平均需要4.8261次攻击才能触发暴击/眩晕
之前连续2次未触发,之后平均需要4.1568次攻击才能触发暴击/眩晕
之前连续3次未触发,之后平均需要3.6702次攻击才能触发暴击/眩晕
之前连续4次未触发,之后平均需要3.21次攻击才能触发暴击/眩晕
之前连续5次未触发,之后平均需要2.8265次攻击才能触发暴击/眩晕
之前连续6次未触发,之后平均需要2.4924次攻击才能触发暴击/眩晕
之前连续7次未触发,之后平均需要2.1826次攻击才能触发暴击/眩晕